[☰][2018-06-30]math:Generating bounded polygons(part 1)
What?
I have recently been really interested in making efficient alghorithms for graphics creation. In particular creating bounded polygons. That is - polygons where the beginning ties to the end and lines don't cross(so you don't have areas with 0 area). To this we add 2 other constraints - we construct them from lines with equal fixed length and we allow only 90 degree angles. The end goal is to come up with a closed form formula for producing polygons of any N lines. Also we are working in the 2d plain. Here are some examples of what I am talking about:
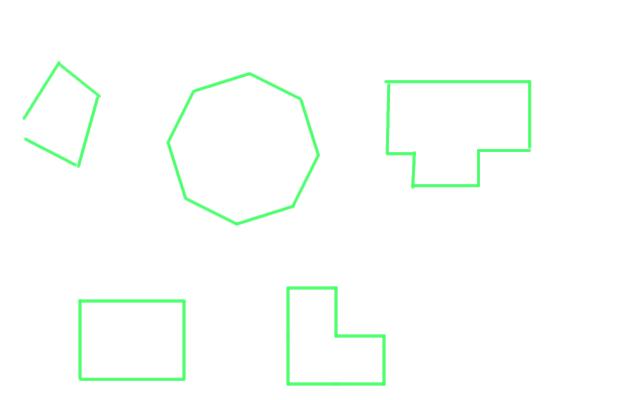
Top row contains only invalid polygons. From left to right 1st one is not bounded, 2nd contains angles different than 90 degrees and 3rd has is made up of lines of unequal length. The bottom row is valid. 1st one is made up of 4 equal lines(square) and the second one of 8 equal lines.
L-systems
The current alghorithm is relatively simple. We start out by introducing a abstraction on top of the target polygons so that we leave geometric space and enter algebraic space. In this case a L-system or Lindenmayer system is a very neat abstract language for describing patterns. We have an initial sequence called an axiom. For example we can have the sequence ABC. Each letter is an action that does something like A can mean push a button, B can be trigger water irrigation. C can mean create AB in next step so we'll have ABAB in second generation. This "replication" is called a rule. A rule determains if an action, when processed will rewrite itself with another set of actions. This is very useful for describing organic compositions such a nature-looking tree or flower petals, etc. In our case we have a very simple alphabet consisting of F, R and L. F draws a line in the given direction(direction defaults to 3 o'clock), R turns direction 90 degrees to the right, L turns direction 90 degrees to the left. So we can have:
FRFRFRF
We draw line forward, turn to the right, draw, etc. until we get a square. This axiom meets all our constraints. This is how the target polygon should "look" like.
Algorithm
The first very important observation is that for each line drawn we can take a decision to flip direction. So for example if we take our square example we can have F_F_F_F for n=4 we have n-1 placeholders that can have R,L or nothing(denoted with _ here). So for N lines polygons we generate the product of all possible combinations of n-1 _,R,L like so:
list(product("_RL", repeat=4))
which will produce things like ('_', '_', '_') which will produce a straight line of length 4 on the screen. Not a valid polygon. Another one is the familiar ('R', 'R', 'R') which makes a square. We obviously need to filter the valid cases from invalid ones. To do that we traverse all actions for an axiom and detect if the beginning will match with the end. We also keep a record of positions and track to not have the same ones (except the initial one) which constitutes a cross To trace them we create a virtual coordinate system with initial coordinates 0,0. When traversing we keep track of the current coordinates and history for cross detection. So with FRFRFRF we have 0,0 → 1,0 → 1,-1 → 0,-1 → 0,0. Beginning matches the end and we don't have repeating coordinates so this one stays in the final set.
Second observation is you cannot have a bounded polygon made up of odd number of equal length lines with 90 degree angles only.
Demo
You can check out the project here. Also here is a video of generating polygons for n=12:

Future
There is still filtering for symmetric shapes. So for example FRFRFRF and FLFLFLF are equivalent and only one of them should remain in the final set. Also there is compressing the whole thing down to a closed form expression. Hopefully in Part 2.